高考函数试题_高考函数例题

1.高三函数题

抽象函数

一般形式为 y=f(x)且无法用数字和字母表示出来的函数，一般出现在题目中，或许有定义域、值域等。

1抽象函数常常与周期函数结合，如：

f(x)=-f(x+2)

f(x)=f(x+4)

2解抽象函数题，通常要用赋值法，而且高考数学中，常常要先求F（0） F（1）

抽象函数的经典题目！！！

我们把没有给出具体解析式的函数称为抽象函数。由于这类问题可以全面考查学生对函数概念和性质的理解，同时抽象函数问题又将函数的定义域，值域，单调性，奇偶性，周期性和图象集于一身，所以在高考中不断出现；如2002年上海高考卷12题，2004年江苏高考卷22题，2004年浙江高考卷12题等。学生在解决这类问题时，往往会感到无从下手，正确率低，本文就这类问题的解法谈一点粗浅的看法。

一．特殊值法:在处理选择题时有意想不到的效果。

例1 定义在R上的函数f(x)满足f (x + y) = f (x) + f ( y )(x，y∈R)，当x<0时，, f (x)>0，则函数f (x)在[a,b]上 ( )

A 有最小值f (a) B有最大值f (b) C有最小值f (b) D有最大值f ( )

分析：许多抽象函数是由特殊函数抽象背景而得到的，如正比例函数f (x)= kx(k≠0)， , , ，可抽象为f (x + y) = f (x) +f (y)，与此类似的还有

特殊函数 抽象函数

f (x)= x f (xy) =f (x) f (y)

f (x)=

f (x+y)= f (x) f (y)

f (x)=

f (xy) = f (x)+f (y)

f (x)= tanx f(x+y)=

此题作为选择题可采用特殊值函数f (x)= kx(k≠0)

∵当x <0时f (x) > 0即kx > 0。.∴k < 0，可得f (x)在[a,b]上单调递减，从而在[a,b]上有最小值f(b)。

二．赋值法．根据所要证明的或求解的问题使自变量取某些特殊值，从而来解决问题。

例2 除了用刚才的方法外,也可采用赋值法

解:令y = -x，则由f (x + y) = f (x) + f (y) (x，y∈R)得f (0) = f (x) +f (-x)…..①,

再令x = y = 0得f(0)= f(0)+ f(0)得f (0)=0，代入①式得f (-x)= -f(x)。

得 f (x)是一个奇函数，再令 ，且 。

∵x <0，f (x) >0，而 ∴ ，则得 ，

即f (x)在R上是一个减函数，可得f (x)在[a,b]上有最小值f(b)。

例3 已知函数y = f (x)(x∈R，x≠0)对任意的非零实数 ， ，恒有f( )=f( )+f( ),

试判断f(x)的奇偶性。

解：令 = -1， =x，得f (-x)= f (-1)+ f (x) ……①为了求f (-1)的值，令 =1， =-1，则f(-1)=f(1)+f(-1),即f(1)=0,再令 = =-1得f(1)=f(-1)+f(-1)=2f(-1) ∴f(-1)=0代入①式得

f(-x)=f(x),可得f(x)是一个偶函数。

三．利用函数的图象性质来解题：

抽象函数虽然没有给出具体的解析式，但可利用它的性质图象直接来解题。

抽象函数解题时常要用到以下结论：

定理1：如果函数y=f(x)满足f(a+x)=f(b-x)，则函数y=f(x)的图象关于x= 对称。

定理2：如果函数y=f(x)满足f(a+x)=f(b+x)，则函数y=f(x)是一个周期函数，周期为a-b。

例4 f(x)是定义在R上的偶函数，且f(x)=f(2-x)，证明f(x)是周期函数。

分析：由 f(x)=f(2-x)，得 f(x)的图象关于x=1对称，又f(x)是定义在R上的偶函数，图象关于y轴对称，根据上述条件，可先画出符合条件的一个图，那么就可以化无形为有形，化抽象为具体。从图上直观地判断，然后再作证明。

由图可直观得T=2,要证其为周期函数，只需证f (x) = f (2 + x)。

证明：f (x) = f (-x) = f [2-(-x)] = f (2 + x)，∴ T=2。

∴f (x)是一个周期函数。

例5 已知定义在[-2，2]上的偶函数，f (x)在区间[0，2]上单调递减，若f (1-m)<f (m),求实数m的取值范围

分析：根据函数的定义域，-m，m∈[-2,2]，但是1- m和m分别在[-2，0]和[0，2]的哪个区间内呢？如果就此讨论，将十分复杂，如果注意到偶函数，则f (x)有性质f（-x)= f (x)=f ( |x| )，就可避免一场大规模讨论。

解：∵f (x)是偶函数， f (1-m)<f(m) 可得 ，∴f(x)在[0，2]上是单调递减的，于是 ，即 化简得-1≤m< 。

采纳我的吧

高三函数题

a=2

f(x)=2x+lnx

f'(x)=x+1/x

x=1,f'(1)=2,f(1)=2

切线方程

y-2=2(x-1)

2x-y=0

f'(x)=a+1/x

若a≥0则

f'(x)=a+1/x>0

x>1/a时函数单增

若a<0则

f'(x)=a+1/x>0

无解

故a>0，x>1/a时函数单增

或a=0，x>0时函数单增

（1）集合A={x|f(x)=x}={1,2}

表示当f(x)=x,即ax^2+(b-1)x+c=0时，

两根x1,x2分别为1,2

所以由韦达定理得x1+x2=-(b-1)/a=3

x1*x2=c/a=2

再由f(0)=c=2 解得a=1,b=-2,c=2

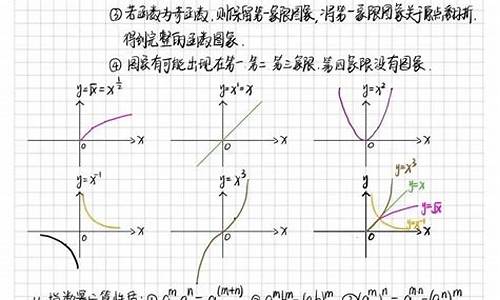
所以f(x)=x^2-2x+2=(x-1)^2+1

由f(x)图像可知:

m=f(x)min=f(1)=1

M=f(x)max=f(-2)=10

(2)集合A={x|f(x)=x}={2}

表示当f(x)=x,即ax^2+(b-1)x+c=0时，

只有唯一的一个根x=2

所以得△=（b-1)^2-4ac=0

且x=-b/2a=2

代入得b=-4a ,c=[(b-1)^2]/4a=4a+1/(4a)+2

则f(x）=ax^2-4ax+4a+1/(4a)+2

因为a≥1，所以可以利用基本不等式

得f(x)≥ax^2-4ax+2[√4a*1/(4a)]+2

=ax^2-4ax+4

对称轴x=-b/2a=-(-4a)/2a=2

由f(x)的图像可知：

m=f(X)min=f(2)=-4a+4

M=f(x)max=f(-2)=12a+4

则 g(a)=M+m=8a+8 (a≥1)

由g(a)的图像可知：g(a)在[1,+∞)上单调递增

所以g(a)min=g(1)=8*1+8=16