高考数学题函数,高考数学题函数题

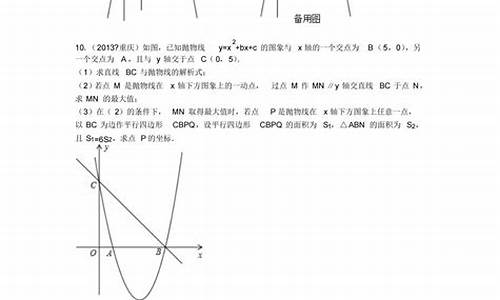
(I)e^x是单调递增函数，因此只要a>0，f(x)就是单调递增函数；

f(x)只与y轴相交，交点A:x=0，y=a；

g(x)=ln(x/a),只与x轴相交，交点B:x=a，g(x)=0;

OAB是等边直角三角形，|AB|=a√2；

点到曲线的距离，与点到直线的距离意义一样，由该点项曲线作“垂线”，点与垂足的连线就是点到该曲线的距离，这个距离在垂足附近最短。这个“垂线”指的是，距离线与垂足处曲线的切线相互垂直。

|AB|是f(x),g(x)上最短距离，意味着，f(x)在A点的切线，g(x)在B点的切线都垂直于AB，AB斜率kAB=(0-a)/(a-0)=-1,切线斜率k=1

f'(x)=ae^x,f'(x)=a=1,

g'(x)=a/x*(1/a)=1/x

g'(a)=1/a=1

a=1

(II)a=1，不等式成为：(x-m)/lnx≥√x，x>0;√x>0;

x=1时，lnx=0，不等式左边无定义，因此以此点分界，分别讨论：

0<x<1时，lnx<0,但是(x-m)/lnx≥√x>0，因此，x-m<0,m>x,必须有m≥1;

(x-m)≤√xlnx，设z=（x-m)-√xlnx≤0；

z'=1-lnx/2√x-√x/x=1-lnx/2√x-1/√x=1-(0.5lnx+1)/√x=1-(ln√x+1)/√x=1-ln[1/(√x)^(√x)]-1/√x

0<x<1;0<√x<1;1/√x>1;0<(√x)^(√x)<1,1/(√x)^(√x)>1,ln[1/(√x)^(√x)]>0;

因此，z'<0,函数递减，只要x->0时，z<0即可；

x->0时，√xlnx是0*∞型不定式，用洛必达法则,先化成∞/∞型，分子分母分别求导：

√xlnx《=》lnx/x^(-0.5)《=》(1/x)/(-0.5x^(-1.5))=-2√x->0,

x->0时，z->-m<0,m>0即可。

因此：m≥1；

x>1时，lnx>0,x-m≥√xlnx>0,x-m>0,m<x,对于所有x>1,恒成立，因此m≤1.

设z=（x-m)-√xlnx≥0；

z'=1-ln[1/(√x)^(√x)]-1/√x

x>1,√x>1,0<1/√x<1,(√x)^(√x)>1,0<1/(√x)^(√x)<1,ln[1/(√x)^(√x)]<0,

z'=1-ln[1/(√x)^(√x)]-1/√x>0,x>1时，z单调递增，只要x->1时，z≥0即可；

x->1,z->1-m≥0,m≤1.

结合起来，m=1；

分析：根据f（x+3）=f（x），确定出函数的周期，再结合函数的奇偶性确定出函数在给定区间上的零点个数，注意找全零点，不能漏掉．

解答：解：由f（x+3）=f（x），得出3是该函数的周期，

由于f（2）=0，若x∈（0，6），

则可得出f（5）=f（2）=0，

又根据f（x）为奇函数，则f（-2）=-f（2）=0，

又可得出f（4）=f（1）=f（-2）=0，

又函数f（x）是定义在R上的奇函数，可得出f（0）=0，

从而f（3）=f（0）=0，在f（x+3）=f（x）中，

令 x=-3/2，得出 f(-3/2)=f(3/2)，

又根据f（x）是定义在R上的奇函数，得出 f(-3/2)=-f(3/2)，

从而得到 f(3/2)=-f(3/2)，即 f(3/2)=0，

故 f(9/2)=f(3/2+3)=f(3/2)=0，

从而 f(9/2)=f(3/2)=f（4）=f（1）=f（3）=f（5）=f（2）=0，若x∈（0，6）．

故答案为：7．