高中理科概率_高考理科概率

1.寻找高考概率题

2.哪位熟悉高中数学的理科高手，帮忙概率统计~

3.高考理科数学统计与概率的大题 都涉及哪方面知识点

4.2012江西一本招生,为什么入取理科的概率是文科概率的4倍?

5.高中数学理科概率

能学的。

如果认真学习，尽管数理化差，但是其它的科目不差的话，我会建议选理科。高考理科比文科录取线相对低很多。选择理科，极大概率可以考上本科。

高考理科比文科录取线相对低很多：

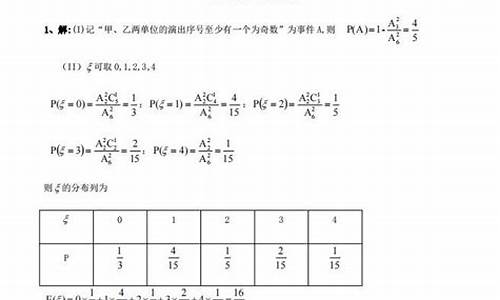
以近年江西高考为例，2019年高考理科与文科本科录取线差别继续拉大，2018年高考理科本科线是447分，文科是496分，理科录取线比文科低了49分。

而2019年高考理科本科录取线是449分，高考文科录取线是502分，理科录取线比文科低了53分，文理科录取线差值比2018年的差值还拉大了4分。按照这个趋势，2020年理科本科线相对文科还要更低一些!

选择理科，极大概率可以考上本科:

如果数理化仅仅是不及格，但不是那种特别差那种，比如说数学考80分左右(高考数学总分150分)，物理55分左右(高考物理总分110分)，化学50分，那么这几门科目合计约为185分左右，语文一般考100分，英语110分，生物相对要好学一些， 多数学生能考出65-70分左右的成绩。

如学生有这样的平均水平，那么高考总分大概是460分左右，这个概率很大，也就是说，这样的考生大概率是可以上理科本科线的。

寻找高考概率题

2023年广西高考数学试题难度适中。

2023年广西高考理科数学试题总体来说有点难度。广西高考理科数学试题整体上难度比较常规，在题目的难度设置上也比较明显。概率题、数列题、填空题就难度较小，立体几何、选择题的7、8题就难度大一些，最难的就是选择题的最后两题、解析几何与倒数的最后一问。

2023广西高考理科数学试题一定也会特别灵活，难度方面会让广西学生表面觉得简单，但又很难下手做。需要广西学生基本功扎实，知识学的灵活，能够随机应变。

2023广西高考理科数学试题难度处于中等偏上，2023广西高考理科数学试卷是全国甲卷。横向比较，甲卷难度甚至高于乙卷，但从历年纵向比较，广西高考理科数学试题难度变化相差不大，但阅读量和计算量确实相较于往年有所增加。

广西高考理科数学试卷试题给出部分已知条件，要求广西考生根据试题要求构建一个命题，给考生充分的选择空间，充分考查学生对数学本质的理解，引导中学数学在数学概念与数学方法的教学中。广西高考理科数学试题重视培养数学核心素养，克服“机械刷题”现象。

高考阅卷：

普通高考的阅卷是实施网上阅卷的方法，当考试结束的时候，省教育考试院将试卷答题卡全部收集起来，先召开阅卷大会，然后将在指定的一所普通高校内的计算机办公大楼组织人员展开阅卷。

答题卡是先拆封后进行扫描录入计算机系统，这一部分将由公安机关单位负责（确保答题卡内容能顺利扫描进计算机系统不被泄露出去），试卷进行切割，选择题部分由工作人员将标准答案录进系统，由计算机自动判别。

解答题和作文部分实行的是人工评分的方式只要是考生回答有理都能获分。阅卷结束的时候，省教育考试院将试卷答题卡重新装订密封进行保管，任何人不得查看，3年后进行销毁处理。

高考试卷的所有客观题批改都是由电脑完成，所有的主观题都实行双评制度，如果两位老师给出的分数差距超出了阈值，那就会自动启动三评程序，如果三评老师给出的分值也超出了阈值，则将启动仲裁程序。

哪位熟悉高中数学的理科高手，帮忙概率统计~

1、(本小题满分12分)某安全生产监督部门对5家小型煤矿进行安全检查(简称安检)．若安检不合格，则必须整改．若整改后经复查仍不合格，则强制关闭．设每家煤矿安检是否合格是相互独立的，且每家煤矿整改前安检合格的概率是0.5，整改后安检合格的概率是0.8，计算(结果精确到0.01)：

(Ⅰ)恰好有两家煤矿必须整改的概率；

(Ⅱ)平均有多少家煤矿必须整改；

(Ⅲ)至少关闭一家煤矿的概率．

2、（本小题满分12分）

甲、乙、丙3人投篮，投进的概率分别是

（I）现3人各投篮1次，求3人都没有投进的概率；

（II）用 表示乙投篮3次的进球数，求随机变量 的概率分布及数学期望

3、（本小题满分12分）

某运动员射击一次所得环数X的分布如下：

X 0-6 7 8 9 10

p 0 0.2 0.3 0.3 0.2

现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为 。

（Ⅰ）求该运动员两次都命中7环的概率：

（Ⅱ）求 的分布列：

（Ⅲ）求 的数学期望E

4、(本小题满分12分)

某安全生产监督部门对5家小型煤矿进行安全检查(简称安检)．若安检不合格，则必须整改．若整改后经复查仍不合格，则强制关闭．设每家煤矿安检是否合格是相互独立的，且每家煤矿整改前安检合格的概率是0.5，整改后安检合格的概率是0.8，计算(结果精确到0.01)：

(Ⅰ)恰好有两家煤矿必须整改的概率；

(Ⅱ)某煤矿不被关闭的概率;

(Ⅲ)至少关闭一家煤矿的概率．

5、（本小题满分12分）

甲，乙，丙三人投篮，投进的概率分别是25，12，35。现3人各投篮1次，求

（Ⅰ）3人都投进的概率；

（Ⅱ）3人中恰有2人投进的概率。

6、（本小题满分12分）

一条生产线上生产的产品按质量情况分为三类： 类、 类、 类. 检验员定时从该生产线上任取2件产品进行一次抽检，若发现其中含有 类产品或2件都是 类产品，就需要调整设备，否则不需要调整. 已知该生产线上生产的每件产品为 类品， 类品和 类品的概率分别为 ， 和 ，且各件产品的质量情况互不影响.

（Ⅰ）求在一次抽检后，设备不需要调整的概率；

（Ⅱ）若检验员一天抽检3次，以 表示一天中需要调整设备的次数，求 的分布列和数学期望.

7、(本小题满分12分)

某商场举行抽奖促销活动，抽奖规则是：从装有9个白球、1个红球的箱子中每次随机地摸出一个球，记下颜色后放回，摸出一个红球可获得奖金10元；摸出两个红球可获得奖金50元．现有甲、乙两位顾客，规定：甲摸一次，乙摸两次．令ξ表示甲、乙两人摸球后获得的奖金总额．求

(1)ξ的分布列； (2)ξ的数学期望．

8、(本小题满分12分)

某商场举行抽奖促销活动，抽奖规则是：从装有9个白球、1个红球的箱子中每次随机地摸出一个球，记下颜色后放回，摸出一个红球获得二等奖；摸出两个红球获得一等奖.现有甲、乙两位顾客，规定：甲摸一次，乙摸两次．求

(1)甲、乙两人都没有中奖的概率；

(2)甲、乙两人中至少有一人获二等奖的概率．

9、（本小题满分12分）

一条生产线上生产的产品按质量情况分为三类： 类、 类、 类.检验员定时从该生产线上任取2件产品进行一次抽检，若发现其中含有 类产品或2件都是 类产品，就需要调整设备，否则不需要调整.已知该生产线上生产的每件产品为 类品， 类品和 类品的概率分别为 ， 和 ，且各件产品的质量情况互不影响.

（Ⅰ）求在一次抽检后，设备不需要调整的概率；

（Ⅱ）若检验员一天抽检3次，求一天中至少有一次需要调整设备的概率.

10、（本小题满分12分）

在添加剂的搭配适用中，为了找到最佳的搭配方案，需要对各种不同的搭配方式作比较，在试制某种牙膏新品种时，需要选用两种不同的添加剂。现在芳香度分别为0，1，2，3，4，5的六种添加剂可供选用。根据实验设计学原理，通常首先要随机选取两种不同的添加剂进行搭配实验。用 表示所选用的两种不同的添加剂的芳香度之和。

（Ⅰ）写出 的分布列：（以列表的形式给出结论，不必写计算过程）

（Ⅱ）求 的数学期望E 。（要求写出计算过程或说明道理）

11、(本小题满分12分)

现有甲、乙两个项目，对甲项目每投资十万元，一年后利润是1.2万元、1.18万元、1.17万元的概率分别为 、 、 ;已知乙项目的利润与产品价格的调整有关,在每次调整中,价格下降的概率都是 ,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为 ,对乙项目每投资十万元, 取0、1、2时, 一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量 、 分别表示对甲、乙两项目各投资十万元一年后的利润.

(I) 求 、 的概率分布和数学期望 、 ;

(II) 当 时,求 的取值范围.

12、（本大题满分12分）

某课程考核分理论与实验两部分进行，每部分考核成绩只记“合格”与“不合格”，两部分考核都是“合格”则该课程考核“合格”，甲、乙、丙三人在理论考核中合格的概率分别为 ；在实验考核中合格的概率分别为 ，所有考核是否合格相互之间没有影响

（Ⅰ）求甲、乙、丙三人在理论考核中至少有两人合格的概率；

（Ⅱ）求这三人该课程考核都合格的概率。（结果保留三位小数）

13、（本大题满分12分）在添加剂的搭配使用中，为了找到最佳的搭配方案，需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时，需要选用两种不同的添加剂。现有芳香度分别为0，1，2，3，4，5的六种添加剂可供选用。根据试验设计原理，通常首先要随机选取两种不同的添加剂进行搭配试验。

（Ⅰ）求所选用的两种不同的添加剂的芳香度之和等于4的概率；

（Ⅱ）求所选用的两种不同的添加剂的芳香度之和不小于3的概率；

14、（本小题满分12分）

甲、乙两班各派2名同学参加年级数学竞赛，参赛同学成绩及格的概率都为0.6，且参赛同学的成绩相互之间没有影响，求：

（1）甲、乙两班参赛同学中各有1名同学成绩及格的概率；

（2）甲、乙两班参赛同学中至少有1名同学成绩及格的概率．

15、（本大题满分12分）

某课程考核分理论与实验两部分进行，每部分考核成绩只记“合格”与“不合格”，两部分考核都是“合格”则该课程考核“合格”，甲、乙、丙三人在理论考核中合格的概率分别为 ；在实验考核中合格的概率分别为 ，所有考核是否合格相互之间没有影响

（Ⅰ）求甲、乙、丙三人在理论考核中至少有两人合格的概率；

（Ⅱ）求这三人该课程考核都合格的概率。（结果保留三位小数）

16、(本小题共13分)

某公司招聘员工，指定三门考试课程，有两种考试方案．

方案一：考试三门课程，至少有两门及格为考试通过；

方案二：在三门课程中，随机选取两门，这两门都及格为考试通过．

设某应聘者对三门指定课程考试及格的概率分别是a，b，c，且三门课程考试是否及格相互之间没有影响．

(Ⅰ)分别求该应聘者用方案一和方案二时考试通过的概率；

(Ⅱ)试比较该应聘者在上述两种方案下考试通过的概率的大小．(说明理由)

17、（本小题满分12分）

A、B是治疗同一种疾病的两种药，用若干试验组进行对比试验.每个试验组由4只小白鼠组成，其中2只服用A，另2只服用B，然后观察疗效，若在一个试验组中，服用A有效的小白鼠的只数比服用B有效的多，就称该试验组为甲类组，设每只小白鼠服用A有效的概率为 ，服用B有效的概率为 。

（Ⅰ）求一个试验组为甲类组的概率。

（Ⅱ）观察3个试验组，用 表示这3个试验组中甲类组的个数，求 的分布列和数学期望。

18、(本小题满分12分)

某射手进行射击训练，设每次射击击中目标的概率为 ，且各次射击的结果互不影响．

(Ⅰ)求射手在3次射击中，至少有两次连续击中目标的概率(用数字作答)；

(Ⅱ)求射手第3次击中目标时，恰好射击了4次的概率(用数字作答)；

(Ⅲ)设随机变量ξ表示射手第3次击中目标时已射击的次数，求ξ的分布列．

19、(本小题共13分)

某公司招聘员工，指定三门考试课程，有两种考试方案．

方案一：考试三门课程，至少有两门及格为考试通过：

方案二：在三门课程中，随机选取两门，这两门都及格为考试通过．

设某应聘者对三门指定课程考试及格的概率分别是0．5，0．6，0．9，且三门课程考试是否及格相互之间没有影响．求：

(Ⅰ)该应聘者用方案一考试通过的概率；

(Ⅱ)该应聘者用方案二考试通过的概率．

20、(本小题满分12分)

A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验,每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效,若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组.设每只小白鼠服用A有效的概率为 ,服用B有效的概率为 .

(Ⅰ)求一个试验组为甲类组的概率；

(Ⅱ)观察3个试验组，求这3个试验组中至少有一个甲类组的概率.

21、(本小题满分12分)

甲、乙两台机床相互没有影响地生产某种产品，甲机床产品的正品率是0.9，乙机床产品的正品率是0.95.

(Ⅰ)从甲机床生产的产品中任取3件，求其中恰有2件正品的概率(用数字作答)；

(Ⅱ)从甲、乙两台机床生产的产品中各任取1件，求其中至少有1件正品的概率(用数字作答).

22、（本小题满分12分）

某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，再从每箱中任意抽取2件产品进行检验。设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品。

（I）用 表示抽检的6件产品中二等品的件数，求 的分布列及 的数学期望；

（II）若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批产品被用户拒绝购买的概率。

23、甲、乙两袋装有大小相同的红球和白球，甲袋装有2个红球，2个白球；乙袋装有2个红球，n个白球，现从甲、乙两袋中各任取2个球。

（Ⅰ）若n=3，求取到的4个球全是红球的概率；

（Ⅱ）若取到的4个球中至少有2个红球的概率为 ，求n.

24、（本小题满分12分）

每次抛掷一枚骰子（六个面上分别标以数字

（I）连续抛掷2次，求向上的数不同的概率；

（II）连续抛掷2次，求向上的数之和为6的概率；

（III）连续抛掷5次，求向上的数为奇数恰好出现3次的概率。

25、（本小题满分12分）

某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，再从每箱中任意抽取2件产品进行检验。设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品。

（I）求取6件产品中有1件产品是二等品的概率。

（II）若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批

产品被用户拒绝的概率。

26、甲、乙两袋装有大小相同的红球和白球，甲袋装有2个红球，2个白球；乙袋装有2个红球，n个白球．现从甲、乙两袋中各任取2个球．

(Ⅰ)若n=3，求取到的4个球全是红球的概率；

(Ⅱ)若取到的4个球中至少有2个红球的概率为 ，求n．

27、（本小题满分10分）

在某校举行的数学竞赛中，全体参赛学生的竞赛成绩近似服从正态分布N（70，100）。已知成绩在90分以上（含90分）的学生有12名。

（Ⅰ）试问此次参赛的学生总数约为多少人？

（Ⅱ）若该校奖励竞赛成绩排在前50名的学生，试问设奖的分数线约为多少分？

可供查阅的（部分）标准正态分布表 （x0）=P(x＜x0）

28、(本小题满分12分)

袋中装着标有数字1，2，3，4，5的小球各2个．从袋中任取3个小球，按3个小球上最大数字的9倍计分，每个小球被取出的可能性都相等，用ξ表示取出的3个小球上的最大数字，求：

(Ⅰ)取出的3个小球上的数字互不相同的概率；

(Ⅱ)随机变量ξ的概率分布和数学期望；

(Ⅲ)计分介于20分到40分之间的概率．

29、（本小题满分13分）

某大厦的一部电梯从底层出发后只能在第18、19、20层可以停靠。若该电梯在底层载有5位乘客，且每位乘客在这三层的每一层下电梯的概率均为 ，用 表示这5位乘客在20层下电梯的人数，求：

（Ⅰ）随即变量 的分布列；

（Ⅱ）随即变量 的期望；

30、（本小题满分12分）

某单位最近组织了一次健身活动，活动分为登山组和游泳组，且每个职工至多参加了其中一组，在参加活动的职工中，青年人占42.5%，中年人占47.5%，老年人占10%。登山组的职工占参加活动总人数的 ，且该组中，青年人占50%，中年人占40%，老年人占10%。为了了解各组不同年龄层次的职工对本次活动的满意程度，现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本，试确定

（Ⅰ）游泳组中，青年人、中年人、老年人分别所占的比例；

（Ⅱ）游泳组中，青年人、中年人、老年人分别应抽取的人数。

31、（本小题满分12分）

盒中装着标有数字1，2，3，4的卡片各2张，从盒中任意任取3张，每张卡片被抽出的可能性都相等，求：

(Ⅰ)抽出的3张卡片上最大的数字是4的概率；

(Ⅱ)抽出的3张中有2张卡片上的数字是3的概率；

(Ⅲ)抽出的3张卡片上的数字互不相同的概率.

32、（本小题满分13分）

甲、乙、丙三人在同一办公室工作，办公室里只有一部电话机，设经该机打进的电话

是打给甲、乙、丙的概率依次为 、 、 .若在一段时间内打进三个电话，且各个电话相互独立.

求：

(Ⅰ)这三个电话是打给同一个人的概率；

(Ⅱ)这三个电话中恰有两个是打给甲的概率

答案放不下了 你在追问一下 把答案发给你

高考理科数学统计与概率的大题 都涉及哪方面知识点

概率统计复习题

1, 有三个箱子,分别编号为1,2,3. 1号箱装有1个红球4个白球,2号箱装有2红3白球 , 3号箱装有3 红球. 某人从三箱中任取一箱,从中任意摸出一球,求取得红球的概率.

2, 甲、乙、丙三人同时对飞机进行射击, 三人击中的概率分别为0.4、0.5、0.7. 飞 机被一人击中而击落的概率为0.2,被两人击中而击落的概率为0.6, 若三人都击中, 飞机必定被击落, 求飞机被击落的概率.

3, 有三个箱子，分别编号为1,2,3，1号箱装有1个红球4个白球，2号箱装有2红球3白球，3号箱装有3红球. 某人从三箱中任取一箱，从中任意摸出一球，发现是红球,求该球是取自1号箱的概率 .

4, 商店论箱出售玻璃杯,每箱20只,其中每箱含0，1，2只次品的概率分别为0.8, 0.1, 0.1，某顾客选中一箱，从中任选4只检查，结果都是好的，便买下了这一箱.问这一箱含有一个次品的概率是多少？

5, 市场上有甲、乙、丙三家工厂生产的同一品牌产品，已知三家工厂的市场占有率分别为1/4、1/4、1/2，且三家工厂的次品率分别为 2％、1％、3％，试求市场上该品牌产品的次品率。

6, 设 X的密度函数是, 求 Y=2X+8 的概率密度.

7，设随机变量X的分布律为：

X －2 －1 0 1 3

P 1/5 1/6 1/5 1/15 11/30

求Y=X 2的分布律

8，

9，设(X,Y)的概率密度是

求 (1) c的值； （2）两个边缘密度。

（3） 判断X,Y是否独立？

10，设随机向量(X,Y)的概率密度函数为

试判断X和Y是否相互独立.

11，若 X 和 Y 相互独立,它们分别服从参数为 的泊松分布, 证明Z=X+Y服从参数为

的泊松分布.

12，

13 并求2X+3的分布率。

14，设X1,X2,…Xn是取自总体 X~B(1, p) 的一个样本，求参数p的最大似然估计量.

15，设总体 X 在 [ a , b ] 上服从均匀分布 , a , b 未知, .X1, X2……Xn 是来自 X 的样本 , 试求 a , b 的矩估计量 .

16, 设某零件的长度X服从正态分布N(μ,0.42). 现在从中抽取20只,测得其平均长度为32.3毫米. 求其长度的置信度为95%的置信区间.

17, 有一大批糖果.现从中随机地取 16 袋 , 称得重量(以克计)如下:

506 508 499 503 504 510 4 512

514 505 493 496 506 502 509 496

设袋装糖果的重量近似地服从正态分布,试求总体均值 的置信水平0.95为的置信区间.

18微波炉在炉门关闭时的辐射量是一个重要的质量指标.某厂该质量指标服从正态分布，长期以来，且均值都符合要求不超过0.12，为检查近期产品的质量，抽查了25台，得其炉门关闭时的辐射量的均值。试问在水平上炉门关闭时的辐射量是否升高了？

19, 某糖厂用自动打包机打包，每包标准重量为100 公斤，每天开工后需检验一次打包机是否正常工作，某日开工后测得九包重量为

99.3，98.7，100.5，101.2，98.3，99.7，99.5，102.1，100.5

设每包的重量服从正态分布.在显著性水平为下，打包机工作是否正常？

20

2012江西一本招生,为什么入取理科的概率是文科概率的4倍?

70%高1,高230%高三每个省份都不同，建议看看近几年的试卷，觉得很多题目其实不是很容易分清属于哪部分的。函数的知识几乎每道题都要用到，而且与解析几何以及向量都有密不可分的联系，可以说是最重要的。数列常会在试卷的难题中作为一小步出现。立体几何和概率一般有一道大题，但一般来说不是很难。三角函数常作为选择或大题中的小步骤出现，不过也做过第一道大题出三角的。另外，一些要求不是很高的知识点，如复数，常会出一两道的选择填空。

高中数学理科概率

首先，你看到录取的同时，也应该看到高考文理人数的悬殊。第二，国家普遍对理工类人才需求更多一些。第三，我个人觉得，理科生不一定学不了文科生的东西，但是文科生很难学好理工类的东西。当然，不是绝对的哈~~谢谢，同意请纳，有意见，可以问我~~

理科考前不比再研究题目了。只要把会的做对就可以了，偶尔把不会的蒙对那就是超长发挥了。

分类别要清晰：

胜的概率：

胜三局：（1/3*1/3*1/3*2/3*2/3)*10 = 40/243 //10 = C3 5

胜四局：（1/3*1/3*1/3*1/3*2/3)*5 = 10/243 //5 = C 4 5

胜五局： (1/3)^5 = 1/243 // 1 = C 5 5 省略不写

总和：51/243

输的概率：

输三局：（1/3*1/3*2/3*2/3*2/3)*10 = 80/243

输四局：（1/3*2/3*2/3*2/3*2/3)*5 = 80/243

输五局： (2/3)^5 = 32/243

总和：192/243

这样输赢的概率相加正好等于1。

试问楼上的哪个做对了?不要误人子弟。