您现在的位置是: 首页 > 教育政策 教育政策
空间向量高考题_空间向量高考题型专题
tamoadmin 2024-05-23 人已围观
简介用向量法求二面角大小,主要是用公式cosA=a*b/(|a|*|b|)a,b要分别取这构成二面角的两个平面的法向量,可能不止一个,取最简单的那个,然后两分别算出它们的模,即|a|,|b|,再代入公式即可算出cosA的值后,再根据前面的判断若是锐角,而算得cosA>0,则所求角为A若是锐角,而算得cosA<0,则所求角为(派-A)若是钝角,而算得cosA>0,则所求角为(派-A)若
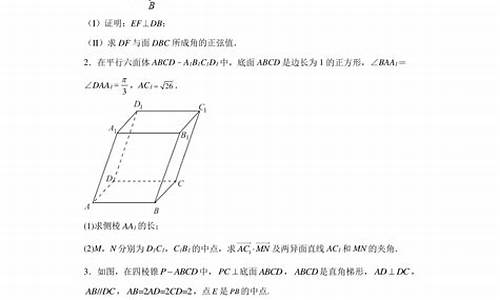
用向量法求二面角大小,主要是用公式
cosA=a*b/(|a|*|b|)
a,b要分别取这构成二面角的两个平面的法向量,可能不止一个,取最简单的那个,然后两分别算出它们的模,即|a|,|b|,再代入公式即可
算出cosA的值后,再根据前面的判断
若是锐角,而算得cosA>0,则所求角为A
若是锐角,而算得cosA<0,则所求角为(派-A)
若是钝角,而算得cosA>0,则所求角为(派-A)
若是钝角,而算得cosA<0,则所求角为A
注:A就是所选的两个法向量的夹角。
扩展资料以下用向量法求解的简单常识:
1、空间一点P位于平面MAB的充要条件是存在唯一的有序实数对x、y,使得PM=xPA+yPB
2、对空间任一点O和不共线的三点A,B,C,若:OP=xOA+yOB+zOC?(其中x+y+z=1),则四点P、A、B、C共面.
3、利用向量证a∥b,就是分别在a,b上取向量a=λb(λ∈R).
4、利用向量证a⊥b,就是分别在a,b上取向量a·b=0 .
百度百科-空间向量
文科可以用空间向量解立体几何题的。
空间中具有大小和方向的量叫做空间向量。向量的大小叫做向量的长度或模(moduius)。
规定,长度为0的向量叫做零向量,记为0.
模为1的向量称为单位向量。
与向量a长度相等而方向相反的向量,称为a的相反向量。记为-a
方向相等且模相等的向量称为相等向量。
1共线向量定理
两个空间向量a,b向量(b向量不等于0),a∥b的充要条件是存在唯一的实数λ,使a=λb
2共面向量定理
如果两个向量a,b不共线,则向量c与向量a,b共面的充要条件是:存在唯一的一对实数x,y,使c=ax+by
3空间向量分解定理
如果三个向量a、b、c不共面,那么对空间任一向量p,存在一个唯一的有序实数组x,y,z,使p=xa+yb+zc。
任意不共面的三个向量都可作为空间的一个基底,零向量的表示唯一。