高考函数导数,高考导函数题

1.高考导数一般都是第几题

2.高考数学函数求导题

3.导数压轴题求取值范围

4.一道高考的函数导数数学题

5.如何利用导数求解高考数学函数题？

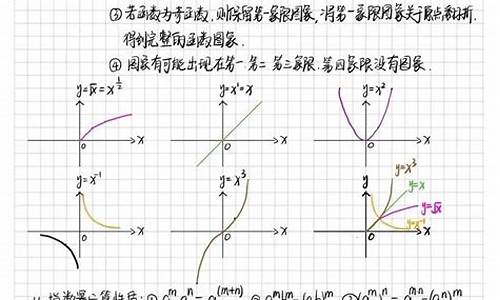
简单的单调性当然不用画表格

但是高考通常不会太简单，画表格是最简明的方式，自己看着方便，批卷老师也一目了然，印象分可能会好一点，当然这样讲可能不科学。至于表格是否好看就不是特别重要了，一旦你养成了画表格的习惯，相信那个时候你的表格会很不错的，到了考场上，你自然会想要一份工整的答卷若果没有明确的单调性说明，老师找不到你的答案，就有可能会误批，画了表格以后，自己继续做题也会很方便。

个人建议画表格，另，祝高考顺利！

高考导数一般都是第几题

其实，高考的导数题就那么几种，lnx—1，ln（x—1），e^x-1,真的，就这么几种，万变不离其中，多做一些题，找规律，什么时候把对数打开，什么时候构造函数，多做题就会有体感。还有一种办法，就是硬求导——分离参数，构造，求导。这种方法很好想，计算量略大，不过顶多求上三次导，肯定行！

高考数学函数求导题

具体题号不一定，至少会有一道选择题和一道压轴大题大题共17分。部分地方出卷还会有相关填空题。

全国卷高考导数题型：

（1）求函数中某参数的值或给定参数的值求导数或切线。

（2）求函数的单调性或单调区间以及极值点和最值。

（3）恒成立或在一定条件下成立时求参数范围。

（4）构造新函数对新函数进行分析。

（5）零点问题。

导数压轴题求取值范围

解，先对fx进行求导，得f’x=3x方+2ax+b因为1和-1是极值点

所以f(1)=f(-1)=0解得a=0,b=-3 所以f'x=3x方-3=3（x方-1） fx=x三次方-3x

故hx=9(3x6次方-9x4次方-10x方+4）-c

对hx求导得h'x=18x5次方-36x3次方-20x)

令其=0解得x=有3个值,

但=0不一定都是极值点,还要逐个验证,也就是极值点的左边和又边在导函数上不能同时大于0或小于0.....如有不懂，请追问

饿.可能有写地方算错了,但思路大概是这样,高三党飘过

一道高考的函数导数数学题

导数压轴题求取值范围如下：

1. 确定函数和参数： 首先，明确你要研究的函数以及函数中涉及的参数。设你的函数是 \(f(x; p)\)，其中 \(x\) 是变量， \(p\) 是参数。

2. 计算函数的导数： 使用适当的导数公式计算函数 \(f(x; p)\) 的导数 \(f'(x; p)\)。这可能涉及链式法则、乘法法则、指数函数的导数规则等。

3. 确定条件：根据问题的背景，确定参数 \(p\) 需要满足的条件。这可能是函数的导数必须为正、函数的导数必须小于某个特定值等。

4. 建立不等式： 使用计算得到的导数公式，将所得的导数与条件进行比较，建立适当的不等式。这将帮助你找到参数 \(p\) 应满足的范围。

5. 解不等式： 解不等式以找到参数 \(p\) 的取值范围。这可能需要代数运算、分析不等式的特性以及使用数学方法来解决不等式问题。

6. 验证范围： 最后，将得到的参数范围代入函数 \(f(x; p)\) 以及其导数 \(f'(x; p)\) 进行验证。确保参数在这个范围内时，函数的性质与要求一致。

拓展：

高考数学导数解题技巧?

1.通过选择题和填空题，全面考查函数的基本概念，性质和图象。

2.在解答题的考查中，与函数有关的试题常常是以综合题的形式出现。

3.从数学具有高度抽象性的特点出发，没有忽视对抽象函数的考查。

4.一些省市对函数应用题的考查是与导数的应用结合起来考查的。

5.涌现了一些函数新题型。

6.函数与方程的思想的作用不仅涉及与函数有关的试题，而且对于数列，不等式，解析几何等也需要用函数与方程思想作指导。

7.多项式求导(结合不等式求参数取值范围)，和求斜率(切线方程结合函数求最值)问题。

8.求极值， 函数单调性，应用题，与三角函数或向量结合。

如何利用导数求解高考数学函数题？

因为当x≠1时，h'(x)<0，所以h(x)是定义域上的减函数，h(x)参考图像如下：

由图像可知

当x∈(0，1)时，h(x)>0；当x∈(1，+∞)时，h(x)<0；

方法的核心就是先对函数两边取对数，然后两边求导，此时要注意等式左边的y的是函数而不是变量，求导时为复合函数求导，求完导数再把左边的y乘到右边，带入y关于x的表达式就得到了y对x的导数