高考函数大小比较_数学高考函数比大小

1.指数函数比较大小口诀

2.对数函数与指数函数如何比大小

3.对数函数怎么比较大小？

4.对数函数比较大小的方法

指数函数比较大小的方法如下：

（1）比差（商）法：（2）函数单调性法；（3）中间值法：要比较A与B的大小，先找一个中间值C，再比较A与C、B与C的大小，由不等式的传递性得到A与B之间的大小。

注意事项：

（1）对于底数相同，指数不同的两个幂的大小比较，可以利用指数函数的单调性来判断。

例如：y1=3^4,y2=3^5，因为3大于1所以函数单调递增（即x的值越大，对应的y值越大），因为5大于4，所以y2大于y1。

（2）对于底数不同，指数相同的两个幂的大小比较，可以利用指数函数图像的变化规律来判断。

指数函数是重要的基本初等函数之一。一般地，y=a^x函数(a为常数且以a>0，a≠1)叫做指数函数，函数的定义域是 R 。注意，在指数函数的定义表达式中，在a^x前的系数必须是数1，自变量x必须在指数的位置上，且不能是x的其他表达式，否则，就不是指数函数。

指数函数是数学中重要的函数。应用到值e上的这个函数写为exp(x)。还可以等价的写为ex，这里的e是数学常数，就是自然对数的底数，近似等于 2.718281828，还称为欧拉数。

指数函数比较大小口诀

一次函数比较y值的大小有两种方法：

（1）根据性质判断：

因为一次函数的解析式是：y=Kx+b，

当K>0时，y随X的增大而增大，

所以当X1>X2时，则y1>y2，反之，当X1<X2时，则y1<y2；

当K<0时，y随X的增大而减少，

所以当X1>X2时，则y1<y2，反之，当X1<X2时，则y1>y2；

（2）根据图象判断：

因为一次函数的图象是一条直线，只要在图象上找出对应点即可；如下图：

对数函数与指数函数如何比大小

指数函数比较大小：比差（商）法；函数单调性法；中间值法。指数函数是重要的基本初等函数之一。

指数函数如何比大小

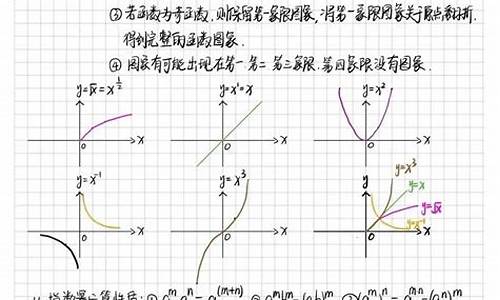
你可以根据图像判断：当底都大于1时，底较大的那个图像陡一些，此时，在第一象限即x>0时，底大的函数值大；在第三象限即x<0时，底小的函数值大；x=0时，函数值都为1.底大于1时函数是增函数。当底都小于1时，底较小的那个图像陡些，此时，在第二象限即x<0时，底小的函数值大；在第四象限即x>0时，底较大的函数值大；x=0时，函数值都为1。底小于1时函数是减函数。

指数函数幂的比较

比较大小常用方法

（1）做差（商）法：A-B大于0即A大于B，A-B等于0即A=B，A-B小于0即A小于B。

步骤：做差—变形—定号—下结论；A\B大于1即A大于B，A\B等于1即A等于B，A/B小于1即A小于B（A，B大于0）

（2）函数单调性法；

（3）中间值法：要比较A与B的大小，先找一个中间值C，再比较A与C、B与C的大小，由不等式的传递性得到A与B之间的大小。

注意事项

比较两个幂的大小时，除了上述一般方法之外，还应注意：

（1）对于底数相同，指数不同的两个幂的大小比较，可以利用指数函数的单调性来判断。

（2）对于底数不同，指数相同的两个幂的大小比较，可以利用指数函数图像的变化规律来判断。

（3）对于底数不同，且指数也不同的幂的大小比较，则可以利用中间值来比较。

<1>对于三个（或三个以上）的数的大小比较，则应该先根据值的大小（特别是与0、1的大小）进行分组，再比较各组数的大小即可。

<2>在比较两个幂的大小时，如果能充分利用“1”来搭“桥”（即比较它们与“1”的大小），就可以快速的得到答案。由指数函数的图像和性质可知“同大异小”。即当底数a和1与指数x与0之间的不等号同向时，a的x次幂大于1，异向时a的x次幂小于1。

对数函数怎么比较大小？

答：对数函数比大小和指数函数比大小的方法如下：

对数比大小

对数的比较主要就是结合图像和利用换底公式。

一、底数相同。

1：底数a>1时，比较真数，真数大的对数大。

2：底数0<a<1时，比较真数，真数大的对数小。

二、底数不相同，真数不相同时。

这种情况下通常采用换底公式，化为相同底数进行比较。

如果不容易化为同一底数，通常有一定技巧。

三、底数不相同，真数相同。

1：底数a>1时，比较底数，底数大的对数小。

2：底数0<a<1时，比较底数，底数大的对数大。

指数函数比大小

指数函数比大小常用方法：

（1）比差（商）法；

（2）函数单调性法；

（3）中间值法；

要比较A与B的大小,先找一个中间值C,再比较A与C、B与C的大小,由不等式的传递性得到A与B之间的大小‘

比较两个幂的大小时,除了上述一般方法之外,还应注意：

（1）对于底数相同,指数不同的两个幂的大小比较,可以利用指数函数的单调性来判断。

（2）对于底数不同,指数相同的两个幂的大小比较,可以利用指数函数图像的变化规律来判断。

（3）对于底数不同,且指数也不同的幂的大小比较,则可以利用中间值来比较.如：

对于三个（或三个以上）的数的大小比较,则应该先根据值的大小（特别是与0、1的大小）进行分组,再比较各组数的大小即可.

在比较两个幂的大小时,如果能充分利用“1”来搭“桥”（即比较它们与“1”的大小）,就可以快速的得到答案.那么如何判断一个幂与“1”大小呢?由指数函数的图像和性质可知“同大异小”.即当底数a和1与指数x与0之间的不等号同向（例如：a 〉1且x 〉0,或0〈 a〈 1且 x〈 0）时,a^x大于1,异向时a^x小于1.。

对数函数比较大小的方法

对数函数比较大小的口诀为：比较函数别着急，对数底数比一比，相同则看单调性，真同最好则换底。俩都不同没关系，中间值来帮助你，1与0看好不好，肯定马上觉容易。

通过对数函数图像判断大小

1、单调性方法，如果是底数一样可以用此方法，底数大于一，函数单增，指数越大，值越大，底数大于零小于一，函数单减，指数越小，值越大。对于对数函数，也是如此。

对于指数函数，如果指数相同，底数不同，实质上应用的是幂函数的单调性。

对于对数函数，如果真数相同，底数不同，如果底数都大于一，那么，告诉你一个规律，对数函数的图像，在x轴以上底数小的在上面，底数大的在下面，在X轴以下相反。这样，画出图像，竖着画一条平行于Y轴的线，就一目了然了。其实，总结一下的话，就是真数相同，底数大于一，底数越小，对数值越大。相反，底数小于一，在x轴以上底数小的在下面，底数大的在上面。

2、对于底数不同，但是真数相同的，可以很快的化同底。举个例子，比如log2.5和log7.5，log2.5=1/log5.2,log7.5=1/log5.7，因为log5.7>log 5.2，所以1/log5.7<1/log5.2，即log7.5<log2.5。

3、找中间值法，一般是对于对数函数而言的，先看正负，若一正一负，自然好，比如lg2和lg0.5.

若为同号，就和1比，如lg8(＜1）和lg12（＞1）

4、有时可以先化简再比较，原则是化为同底数，什么样的对数可以化为同底？这里不要使用换底公式的话，一般是底数或真数同为某个数的幂次才行。

y=logaX?

上下比较：在直线x=1的右侧，a>1时，a越大，图像向右越靠近x轴，0<a<1，a越小，图像向右越靠近x轴。

左右比较：比较图像与y=1的交点，焦点的横坐标越大，对应的函数的底数越大